Department of Mathematics, Statistics
and Computer Science
Wim Ruitenburg's Fall 2004 MATH025.1001
Finite two-player games
We are familiar with all kinds of board games.
Chess, checkers, go, and similar games are examples of two-player games with
`full information.'
Both players can see the full game situation, contrary to many card games
where we may not know the hand of cards held by the other player(s).
Below are two examples of two-player games with `full information'.
Nim
On a table lie a number of piles of matches.
Two players alternatingly must take one or more matches from one, and only one,
of the piles.
The player who takes the last match(es) wins.
Question: Is there a winning strategy for one of the players?
If so, what is it?
- Consider the special case when we start with just one pile of matches.
Then player one has a winning strategy: Simply take all matches.
- Consider the special case when we start with two piles of matches.
There are two possibilities.
- The two piles are of unequal size.
Then the player whose turn it is, takes enough matches from the larger pile so
that both become of equal size.
This will lead to winning the game.
- The two piles are of equal size.
The player is forced to take matches from one pile, and so must make their
sizes different.
If the opponent uses the winning strategy of equaling the sizes, then this
player will lose.
- In class we discussed the strategy for the general situation.
Here we give a very brief sketch.
Think of each pile as a collection of different powers of 2.
For example, if we have piles of sizes 1, 3, 11, and 6 matches, then think of
them as composed of (1), (2+1), (8+2+1), and (4+2) matches.
Alternatively, when we write 1, 3, 11, and 6 in binary notation, we see 1, 11,
1011, and 110.
From right to left, these binary digits record the presence of 1, of 2, of 4,
of 8, of 16, and so on, in the individual numbers 1, 3, 11, and 6.
The winning strategy consists of taking matches from one of the piles such
that the composition has an even number of 1s, an even number of 2s, an even
number of 4s, an even number of 8s, and so on.
In the example above with 1, 3, 11, and 6 matches: The player whose turn it
is should take 7 matches from the pile of size 11, leaving piles of sizes 1, 3,
4, and 6 for the other player.
Note that the piles are now composed of (1), (2+1), (4), and (4+2) matches.
In binary notation, piles of sizes 1, 11, 100, and 110.
Hex
The following two pictures are licensed under the GNU Free Documentation License.
It is material from the Wikipedia article "Hex
Game".
The general board is a diamond-shaped frame of hexagons.
In class we used an 8 by 8 board.
Below is a board of size 11 by 11.
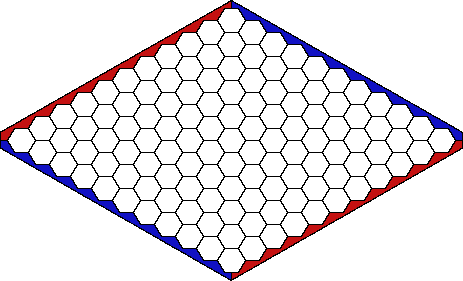 The red and blue players alternatingly put a red stone, respectively a blue
stone, on one of the empty hexagonal fields, without replacement.
A player wins if (s)he creates a connecting path between the sides of his/her
color.
Below is an end situation where red has won.
The red and blue players alternatingly put a red stone, respectively a blue
stone, on one of the empty hexagonal fields, without replacement.
A player wins if (s)he creates a connecting path between the sides of his/her
color.
Below is an end situation where red has won.
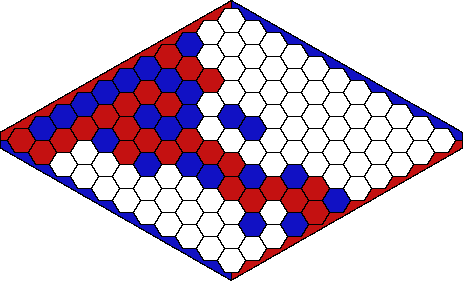 Question: Is there a winning strategy for one of the players?
If so, what is it?
Question: Is there a winning strategy for one of the players?
If so, what is it?
- We mentioned in class that when the game is fully played, then there
must be a path connecting the red sides, or there must be a path connecting the
blue sides.
So no game can end in an involuntary draw.
- Athough the tree diagram of all possible games is gigantic in size, it
is finite.
We observed in class that, by a back-tracking argument, there must be a winning
strategy for one of the players.
- The beginning player, red in the example above, now must have a winning
strategy.
For suppose, to the contrary, that blue has a winning strategy.
Then red can start off by making some random first move, after which it starts
acting as if it is the second player.
In that case, both red and blue have a winning strategy, impossible.
So red has a winning strategy.
- What is the winning strategy for red?
So far nobody knows.
We only know for sure that it exists.
Last updated: October 2004
Comments & suggestions:
wimr@mscs.mu.edu


