Department of Mathematics, Statistics
and Computer Science
Wim Ruitenburg's Fall 2007 MATH025.1001
Mathematical puzzles are more than just recreation, just as child's play is
more than just fun.
Mathematical puzzles are excellent training for problem solving skills.
Mathematical puzzles
We use the book, pages 28-32, as part of the following list of illustrations
about mathematical puzles.
- We started with the word problem:
- The captain of the ship is twice as old as the ship was when the ship
was as old as the captain is now.
Together they are 56 years old.
How old is the captain?
How old is the ship?
In solving this puzzle, we consider naming things, get equations, and then we
still had to find the part of what makes this a puzzle.
- Problem 6 on the 3 switches and the light, is not really a mathematics
problem; its solution needs extra principles from physics.
It is usual for a solution to a puzzle, to need scientific principles from
outside the ones stated in the problem, but they should be kept to a bare
minimum, and be obvious from the context of the problem.
- Problem 3 on buying and selling, is a mathematical puzzle.
It is not too exciting; it looks like a beginning business math textbook
exercise.
- Problem 13 on the cup with tea and the pitcher with cream, is a
mathematical puzzle in the full sense.
Its solution is mathematical, with minimal assumptions from physics.
In fact, its best solution requires almost no mathematics either.
- The following problem is not in the book.
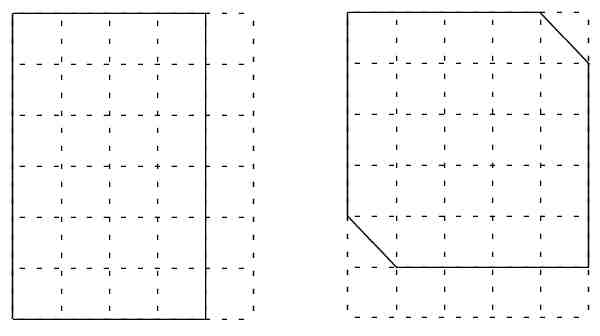
Consider the two pieces of paper below, outlined by solid lines.
The dotted lines are only an auxiliary grid by which we can see that the
first piece of paper is a 4 by 6 rectangle, and the second is a 5 by 5 piece
with two opposite corners clipped.
Problem: Show how to cut one piece into two parts by cutting with a scissors,
so that the other paper can be obtained by putting the two parts together in
another way.
- We seem to make the puzzle above harder by asking to solve the same clip
and paste question for the following two pieces of paper:
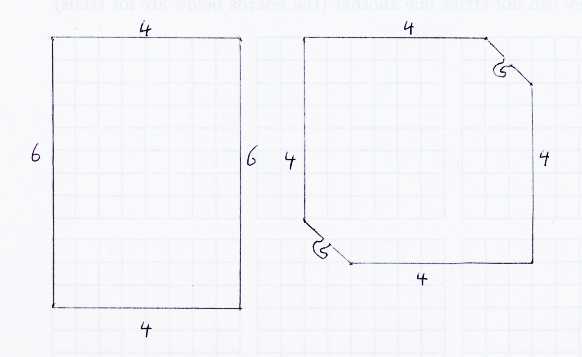 Did we really make it harder?
The more complicated picture on the right leaves so few possibilities to try,
that it should be easier.
Did we really make it harder?
The more complicated picture on the right leaves so few possibilities to try,
that it should be easier.
- We easily cover an 8 by 8 chess board with 32 dominoes each the size of
exactly two fields.
For example, we can line up the dominoes in rows.
There are very many ways by which we can cover the 8 by 8 chess board with 32
such dominoes.
Now for the more complicated puzzle:
From the blue chess board below we cut the top left field and the bottom right
field.
We also throw away one of the dominoes.
Question: Can we cover the damaged blue chess board below with 31 dominoes each
the size of exactly two fields?
Last updated: October 2007
Comments & suggestions:
wimr@mscs.mu.edu



