Department of Mathematics, Statistics
and Computer Science
Wim Ruitenburg's Spring 2010 MATH 1300-101
Mathematical puzzles are more than just recreation, just as child's play is
more than just fun.
Mathematical puzzles are excellent training for problem solving skills.
Mathematical puzzles
- There is a light bulb in a distant room of our home.
All we see before us in our current room are three light switches labeled A, B,
and C.
Exactly one of these controls the light bulb.
It seems that in general (and assuming we are not lucky) that we need two trips
to determine which one of the switches controls the light bulb.
Find a way to solve the problem with guaranteed success, in just one trip.
This problem of the three switches and the bulb, is not purely a mathematics
problem; its solution needs extra principles from physics.
It is usual for a solution to a puzzle, to need scientific principles from
outside the ones stated in the problem, but they should be kept to a bare
minimum, and be obvious from the context of the problem.
- Here is one variation of a classic word problem:
- Two women are sitting at a roadside cafe, talking about family.
One mentions that she has 3 daughters the product of whose ages equals 36.
Remarkably, she mentions, the sum of their ages equals the number on the
house across the street.
The other replies that this is not enough information to find the ages of the 3
daughters.
True, says the one, but note that my oldest daughter has beautiful eyes.
Ah, says the other, but then I know your daughter's ages.
What are the ages of the 3 daughters?
- At the river's edge stand three cannibals and three missionaries.
There is a boat that carries at most two people across at a time.
For the wellbeing of all, at no time are cannibals allowed to outnumber
missionaries on either side or in the boat.
How can we get all six across the river?
Here is a variation:
A farmer wishes to move a fox, a chicken, and corn across the river.
The boat can carry only one of the 3 items at a time.
If left alone, the fox will eat the chicken, and the chicken will eat the
corn.
How does the farmer get all 3 across safely?
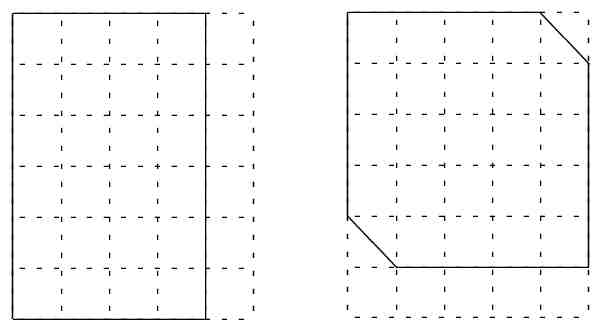
- Consider the two pieces of paper below, outlined by solid lines.
The dotted lines are only an auxiliary grid by which we can see that the
first piece of paper is a 4 by 6 rectangle, and the second is a 5 by 5 piece
with two opposite corners clipped.
Problem: Show how to cut one piece into two parts by cutting with a scissors,
so that the other paper can be obtained by putting the two parts together in
another way.
 We seem to make the puzzle above harder by asking to solve the same clip and
paste question for the following two pieces of paper:
We seem to make the puzzle above harder by asking to solve the same clip and
paste question for the following two pieces of paper:
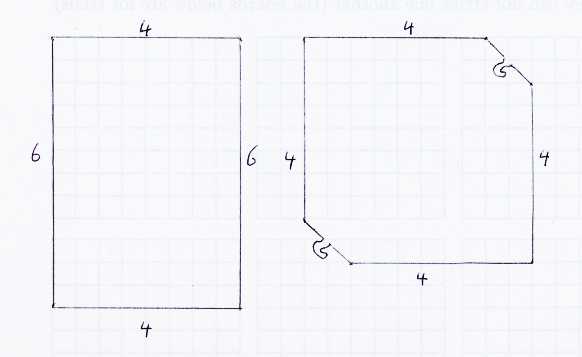 Did we really make it harder?
The more complicated picture on the right leaves so few possibilities to try,
that it should be easier.
Did we really make it harder?
The more complicated picture on the right leaves so few possibilities to try,
that it should be easier.
- Before us lies a row of 100 coins, of all kinds of denominations.
Two players alternatingly are allowed to choose and take one coin, either from
one end of the row or from the other.
Find a general strategy so that the beginning player can be sure to get at
least half the total value of the coins.
- We have a cup with 5 ounces of tea, and a pitcher with 5 ounces of
cream.
We pour some cream into the tea cup.
Then we pour some of the liquid from the tea cup back into the pitcher.
It happens that both tea cup and pitcher again contain 5 ounces each, although
maybe not pure tea or pure cream.
Question:
Did more tea move from cup to pitcher, or did more cream move from
pitcher to cup, or did equal amounts move?
- We easily cover an 8 by 8 chess board with 32 dominoes each the size of
exactly two fields.
For example, we can line up the dominoes in rows.
There are very many ways by which we can cover the 8 by 8 chess board with 32
such dominoes.
Now for the more complicated puzzle:
From the blue chess board below we cut the top left field and the bottom right
field.
We also throw away one of the dominoes.
Question: Can we cover the damaged blue chess board below with 31 dominoes each
the size of exactly two fields?
Last updated: February 2010
Comments and suggestions: Email wimr@mscs.mu.edu

