Wim Ruitenburg's Fall 2012 MATH 1300-101

Marquette University

Department of Mathematics, Statistics and Computer Science

Wim Ruitenburg's Fall 2012 MATH 1300-101

Last updated: December 2012
Comments and suggestions: Email wimr@mscs.mu.edu

Finite two-player games

We are familiar with all kinds of board games. Chess, checkers, go, and similar games are examples of two-player games with `full information.' Both players can see the full game situation, contrary to many card games where we may not know the hand of cards held by the other player(s). Below are examples of two-player games with `full information'.

Nim

We are given some piles of pennies, at least one pile, but usually several piles. Two players alternatingly must take pennies from the piles, subject to the following rules:

Each player takes at least one penny.
Each player takes pennies from at most one pile.

You win when you empty the last pile so that the (losing) player can not make a next move.
Winning strategy: In class we hinted at writing the number of pennies in each pile in binary notation.

The Game of Nimr

The game of nimr is played on a rectangular board, usually a square board of size 8 by 8, or 9 by 9, or 10 by 10, or 11 by 11. We have two players. Let us call them RED and BLUE. Player RED has one red piece in each column; player BLUE has one blue piece in each column. The red pieces are all below the blue pieces. In other words, the blue pieces are all above the red pieces. The initial setup is essentially random. The following is an example.

8
7
6
5
4
3
2
1

The players alternatingly must move one of their pieces to another position in the same column, between their last row and the piece of the opposing player. A player wins when the other gives up, or when the other can no longer move a piece. In general, the choice of who begins is determined by flipping a coin or so.

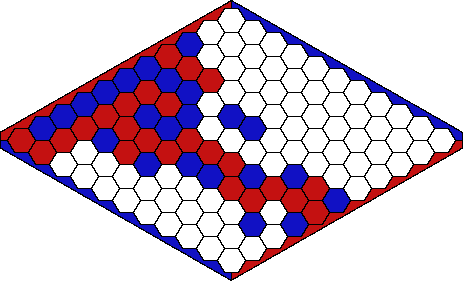
In the example position, let us assume that it is RED's turn to move. Then RED could choose to move A1-A4, that is, move the piece in the bottom left corner three fields up. Or move D4-D3, that is, move the fourth red piece one field back. Note that RED can move its piece on field H5 only backwards.
In the example position if, instead, it were BLUE's turn, then he/she could choose to move C7-C4, or choose to move B5-B6. Note that BLUE can move its piece on field H6 only backwards.

For demonstration purposes, let us briefly work with 5 by 5 boards. Consider the following position with RED's turn to make a move.

Obviously, RED cannot move. So BLUE has won the game.

Consider the following position with BLUE's turn to make a move.

BLUE cannot move. So RED has won.

The following woven handiwork is due to Courtney Tarsa:

Winning Strategies for Nimr

The goal of this project is: Develop a relatively easy winning strategy for each of the players, where possible.

First some partial solutions. Consider the following game situation:

The red and blue pieces in each column touch. Let us call such a setup a kissing position. Suppose it is RED's move. Then there is an easy winning strategy for BLUE. Here is how. All that RED can do is, move one of his/her pieces back. For example, RED can move A4-A2. In reply, BLUE follows RED's piece by moving A5-A3. We again have a kissing position with RED having to move. So BLUE has the easy strategy of creating another kissing position, to which RED can only reply by moving back.

If, in the above position, it were BLUE's turn, then there is the same winning strategy for RED. BLUE is forced to make a move backwards. In response, RED follows in the same column, thereby creating a new kissing position to which BLUE must respond by moving back or by giving up. The kissing position becomes an invariant. Whenever BLUE breaks the invariant, RED restores it.

Let us make the problem slightly harder. Suppose all pieces touch in all columns, except one. For example, consider the situation

Suppose it is the turn of RED. Does he/she have a winning strategy? Yes. Move C1-C3. Then we have a kissing position, while it is BLUE's turn to move. We saw before that RED has a winning strategy; BLUE has lost. Suppose, instead, that in the original situation above, it is the turn of BLUE. Then BLUE has a winning strategy: Move C4-C2. Then BLUE has created a kissing position with RED to move.

We have complete winning strategies in case we have a kissing position, and in case we are one move away from a kissing position. What if there are two columns where the opposite pieces are not immediate neighbors? Let us first look at the case where the two gaps are equal, for example as in:

We have two gaps of equal size 3. Suppose it is RED's turn. Then the following is a winning strategy for BLUE. It will not help RED to make a backward move, because BLUE will simply follow in that same column, and preserve the size of the gap. Whichever forward move RED makes in one column, BLUE does essentially the same in the other. For example, suppose RED moves D2-D3. Then BLUE responds by moving C5-C4. The result is two gaps of equal size 2. And so on.

In the two-column case above, suppose instead that it is BLUE's turn. Then RED has a winning strategy by moving forward and restore two equal gaps (or create a kissing position) whenever BLUE makes a move. So two equal columns (or a kissing position) is an invariant. Whenever BLUE makes a move, it must break the invariant. RED can always respond by a forward move which restores the invariant.

Consider the two-columns case where the gaps are not equal as in:

In this example, the two gaps are of sizes 2 and 3. Suppose it is RED's turn. Then RED has a winning strategy as follows. Move D2-D3, and so create the invariant mentioned above: BLUE faces two gaps of equal size, in this case both of size 2. Conversely, if it had been BLUE's move in the situation with gaps of sizes 2 and 3, then BLUE would have won. His/her first move would have been D6-D5.

We now have complete solutions for when there are at most two columns where opposite pieces are not immediate neighbors. What if we have 3 or more non-neighbor columns? Now it gets more mathematical. Below we give the full winning strategy, which contains the special cases mentioned above. Consider the following starting position:

8
7
6
5
4
3
2
1

We assume that it is RED's turn. To compute potential winning moves, we first list the sizes of the gaps between opposing pieces in each column. The example above gives the list of gap numbers

The number of fields between the red piece on A1 and the blue piece on A8 equals 6. The number of fields between the red piece on H5 and the blue piece on H6 equals 0. In the next step we must make a table with the binary decomposition of each of these eight numbers. This is how. Recall that the numbers 1, 2, 4, 8, 16, 32, 64, 128, and so on are the powers of 2; these numbers are products 2 times 2 times 2 times etcetera, a number of times. Now write each of the eight numbers as a sum of different powers of 2, and put the parts in a table as follows.

6	3	3	2	1	4	5	0
-	1	1	-	1	-	1	-
2	2	2	2	-	-	-	-
4	-	-	-	-	4	4	-
-	-	-	-	-	-	-	-

For example, 6 equals 4 + 2; and 5 equals 4 + 1; and 2 simply equals 2. Strategy for RED: make a forward move such that there are an even number of 8s; an even number of 4s; an even number of 2s; and an even number of 1s.

There are 0 8s, so there are already an even number of 8s.
There are 3 4s, so there are an odd number of 4s.
There are 4 2s, so there are already an even number of 2s.
There are 4 1s, so there are already an even number of 1s.

In this case it suffices if RED removes a 4. Each of the following moves on its own is a winning move for RED:

A1-A5
F1-F5
G2-G6

RED could even choose to make one of the backward moves

E6-E2
H5-H1

Although these are winning moves for RED, they may make the game last longer.

The Game of Hex

The following two pictures are licensed under the GNU Free Documentation License. It is material from the Wikipedia article "Hex Game". The general board is a diamond-shaped frame of hexagons. In class we used a 10 by 10 board. Below is a board of size 11 by 11.

The red and blue players alternatingly put a red stone, respectively a blue stone, on one of the empty hexagonal fields, without replacement. A player wins if (s)he creates a connecting path between the sides of his/her color. Below is an end situation where red has won.

Question: Is there a winning strategy for one of the players? If so, what is it?

We mentioned in class that when the game is fully played, then there must be a path connecting the red sides, or there must be a path connecting the blue sides. So no game can end in an involuntary draw.
Although the tree diagram of all possible games is gigantic in size, it is finite. We observed in class that, by a back-tracking argument, there must be a winning strategy for one of the players.
The beginning player, red in the example above, now must have a winning strategy. For suppose, to the contrary, that blue has a winning strategy. Then red can start off by making some random first move, after which it starts acting as if it is the second player. In that case, both red and blue have a winning strategy, impossible. So red has a winning strategy.
What is the winning strategy for red? So far nobody knows. We only know for sure that it exists.
The following magnetic handiwork is due to Bethdalie Cruz:

Hex on the Web

Some sample websites on Hex, collected with Chris Herrild:
- Follow the link to the games.
- Play or download and play the game.

Example Problem(s)

Suppose we have two piles of pennies in the game of Nim, of sizes 7 and 12. It is your turn. Give a move that keeps you in a winning position.
Suppose we have three piles of pennies in the game of Nim, of sizes 7 and 12 and 7. It is your turn. Give a move that keeps you in a winning position.
Randomly set up 4 or 5 piles of up to 10 pennies. Determine if there is a winning strategy, and if so give a first winning move.